In engineering practice, the evaluation of the Young’s modulus is based on the availability of an unconfined stress vs. strain curve that runs all the way through failure. The Young’s modulus is typically obtained about half-way along that curve.
In petrophysical and geophysical applications, however, knowledge of how strain amplitude and stress conditions influence uniaxial loading stiffness as well as Poisson’s ratio is necessary.
Complexity of YM & PR determination
The data collected in the lab demonstrate how much complexity lies in the determination of the Young’s modulus (YM) and Poisson’s ratio (PR). This data can be used to decide what values should be kept as reference for a given material, before other effects such as complex states of stress can be quantified.
Below 👇 is a simulation hosted on the metaKinetic platform that represents such lab data and provides an interactive estimation of YM and PR.
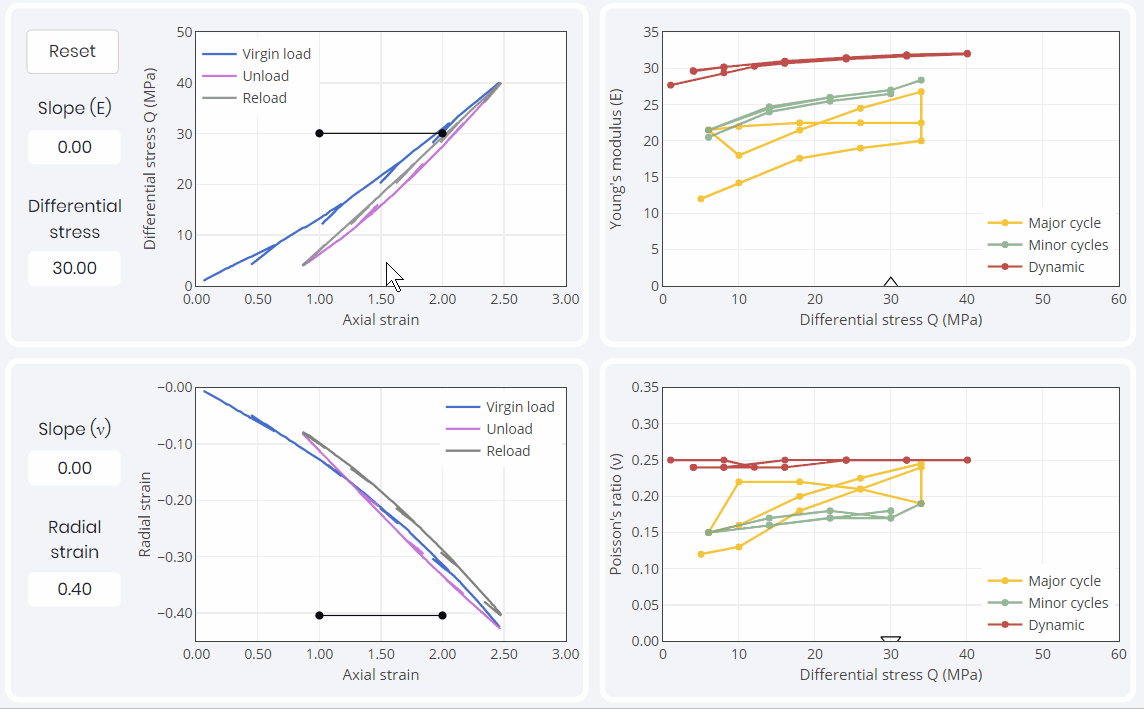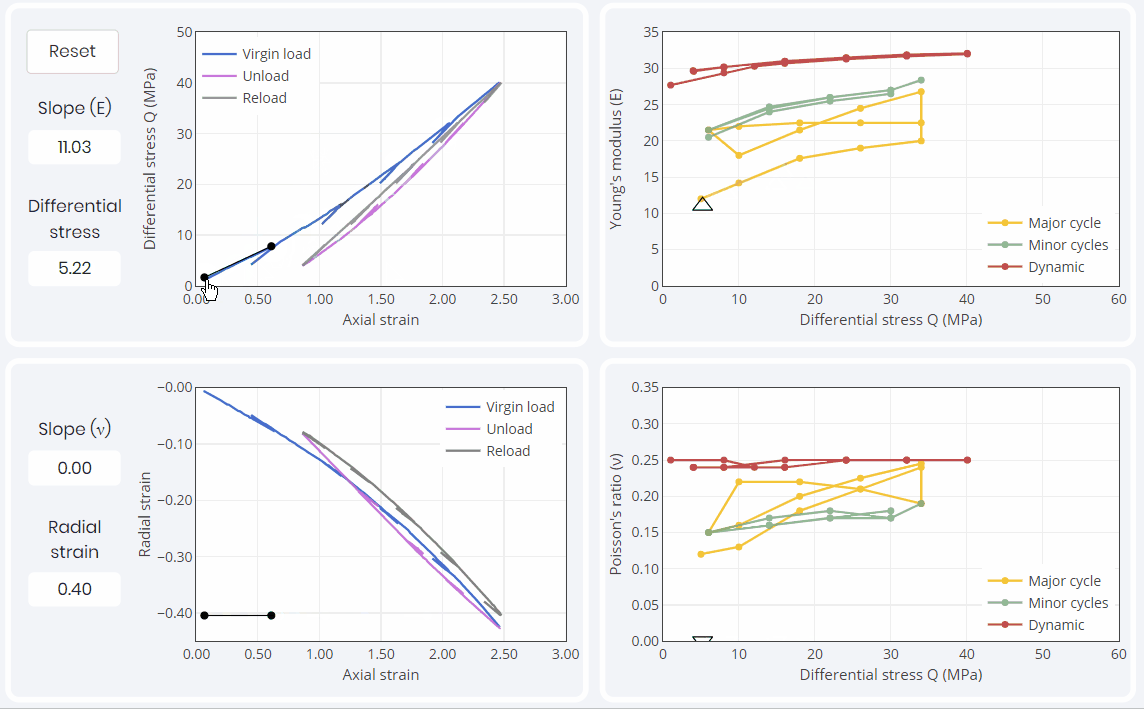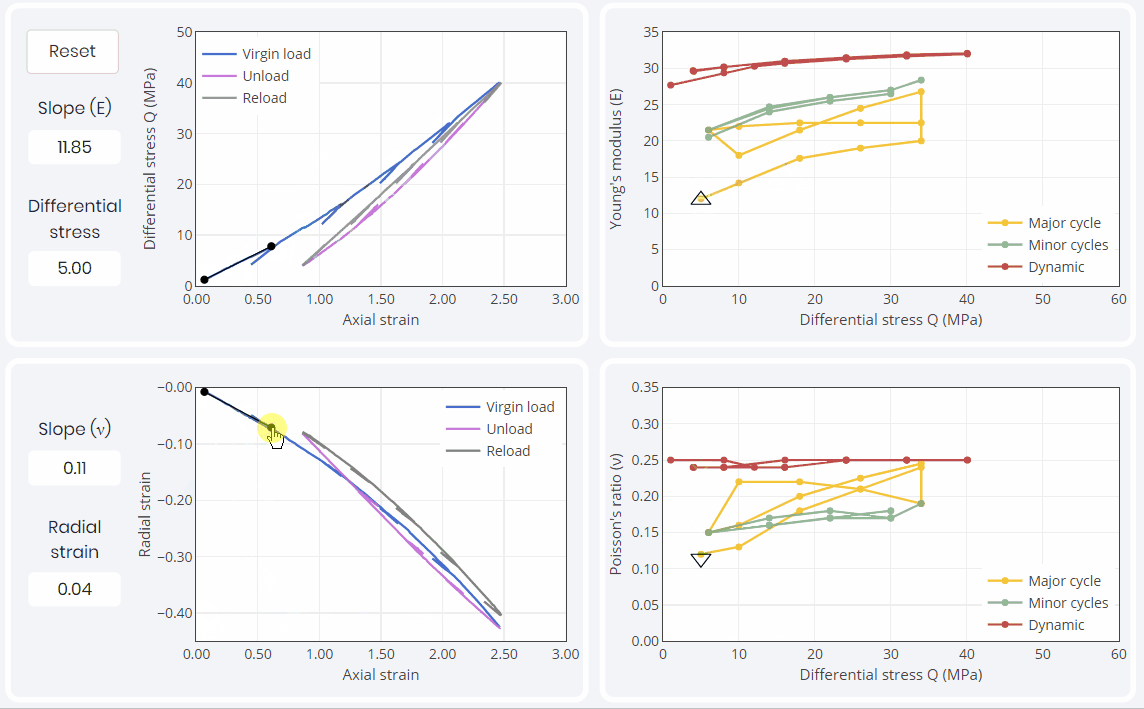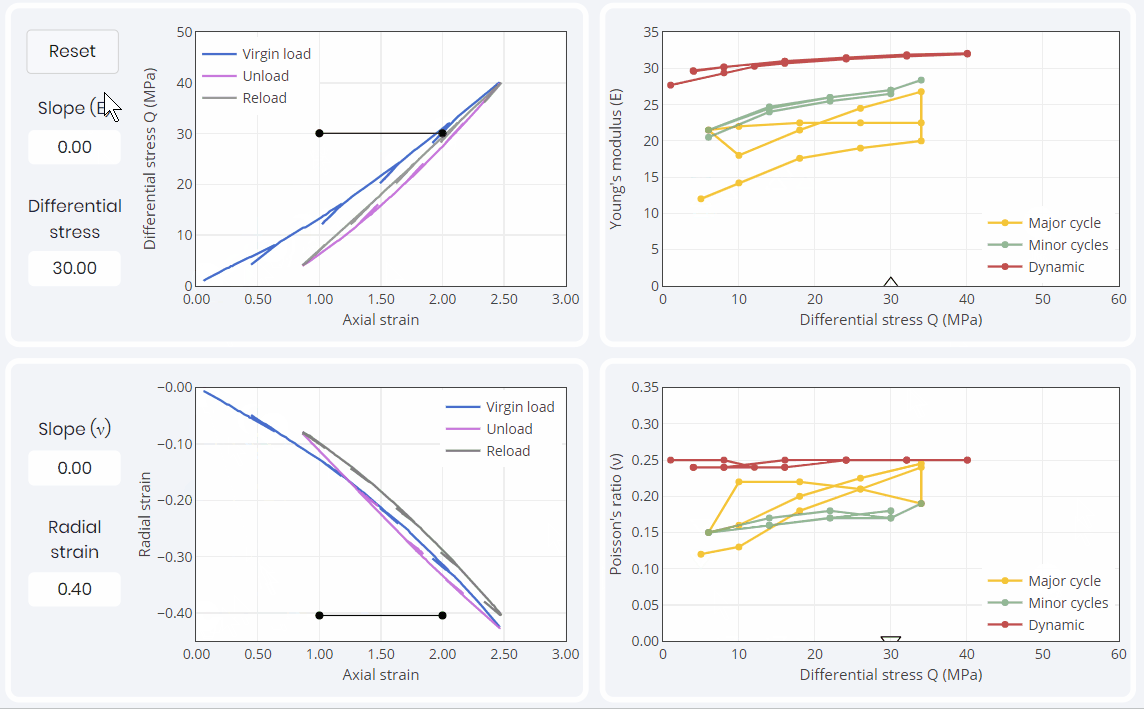
Looking only at the major cycles, the first loading or ‘virgin loading’ is where the smaller Young’s modulus values are traditionally obtained. Upon subsequent unloading and reloading, the samples always exhibit a stiffer behavior up to the highest stress level that was encountered in the first loading.
The low stiffness measured on this initial loading leg is usually related to either:
- The closure of stress relief induced microcracks or other microstructural disturbances,
- Strain hysteresis which causes loading-unloading loops that become more noticeable as strain amplitude increases.
Hysteresis
Hysteresis causes both Young’s modulus and Poisson’s ratio to create ‘bow tie’ patterns as showed in the above simulation in yellow. Though this behavior can be satisfactorily modeled, it is hardly conducive to the definition of a single pair of YM and PR values for a given stress state.
The moduli obtained during the small unloading and reloading cycles shown in green appear to be independent on the loading cycle in which they were measured. Those moduli not only are independent of the loading cycle but also are the only ones that actually qualify as linear elastic moduli as they exhibit a reversible stress-strain behavior. Therefore, these small perturbation moduli are the ones that one should focus on in a first instance. They can constitute ‘seeds’ from which a more complex behavior (i.e. accounting for hysteresis) can be modeled if desired.
Where is the difference between the static and dynamic moduli coming from?
This mostly is attributable to the difference between drained and undrained behaviors. In drained conditions, the deformation is slow enough to allow saturating fluids to move through the pore network without affecting the stiffness. In undrained conditions, the high strain rate associated with the propagating wave mostly precludes fluid motion which results in the fluid directly contributing to the overall stiffness by an amount commensurate with its bulk modulus scaled by the rock porosity. In the absence of a saturating fluid, the small perturbation static moduli can fall very close to the dynamic ones. Keep in mind that many other parameters can strongly influence these results such as fluid type, fluid saturation level, and material anisotropy.
Laurent Louis, Scientific Advisor
Contact us if you would like to access this simulation and more on the metaKinetic platform.
