Fourier Transform is a mathematical process of matching distinct and simple sine functions to another function, in order to discover the underlying spectral components of that function. Fourier Transform comes in different forms, including the analytic, analog, simply known as Fourier Transform (FT), the basic digital version known as discrete Fourier transform (DFT), and the more efficient digital version called the fast Fourier transform (FFT). FFT is used in any application that involves signal processing.
The FFT algorithm makes the spectral analysis of signals fast, easy and efficient. To demonstrate the value of the FFT application in signal filtering, now there is a new simulation on metaKinetic Seismic Reflection Gallery.
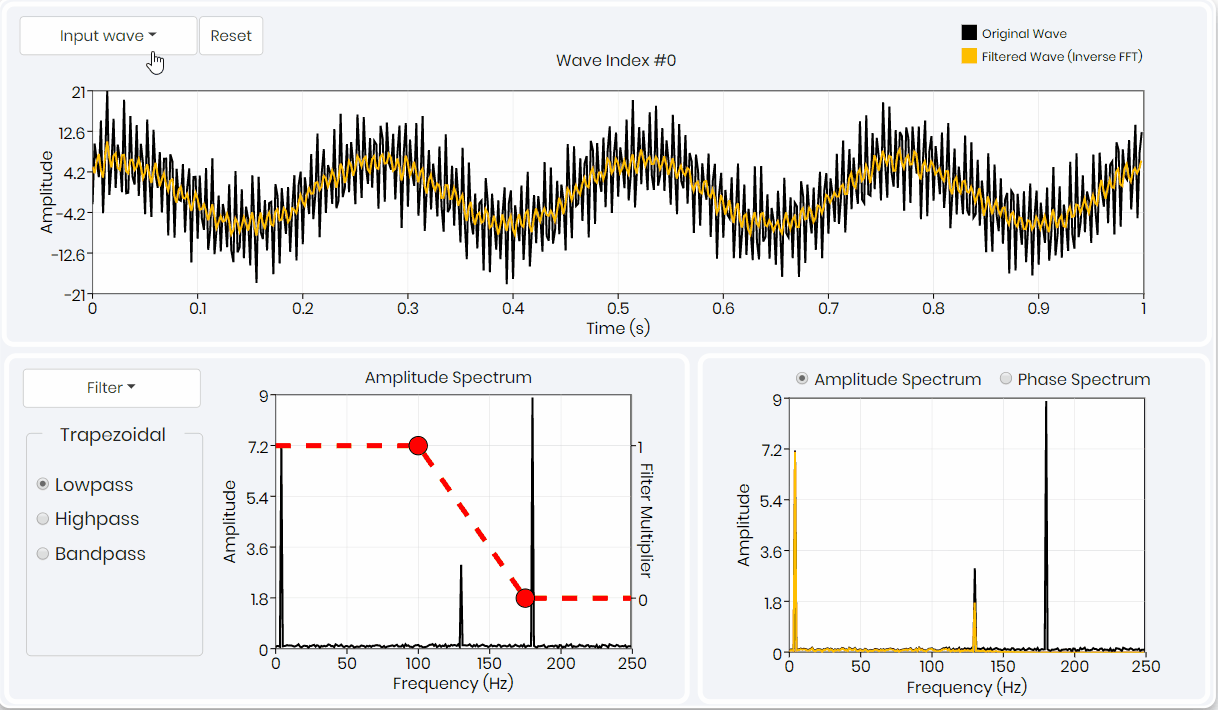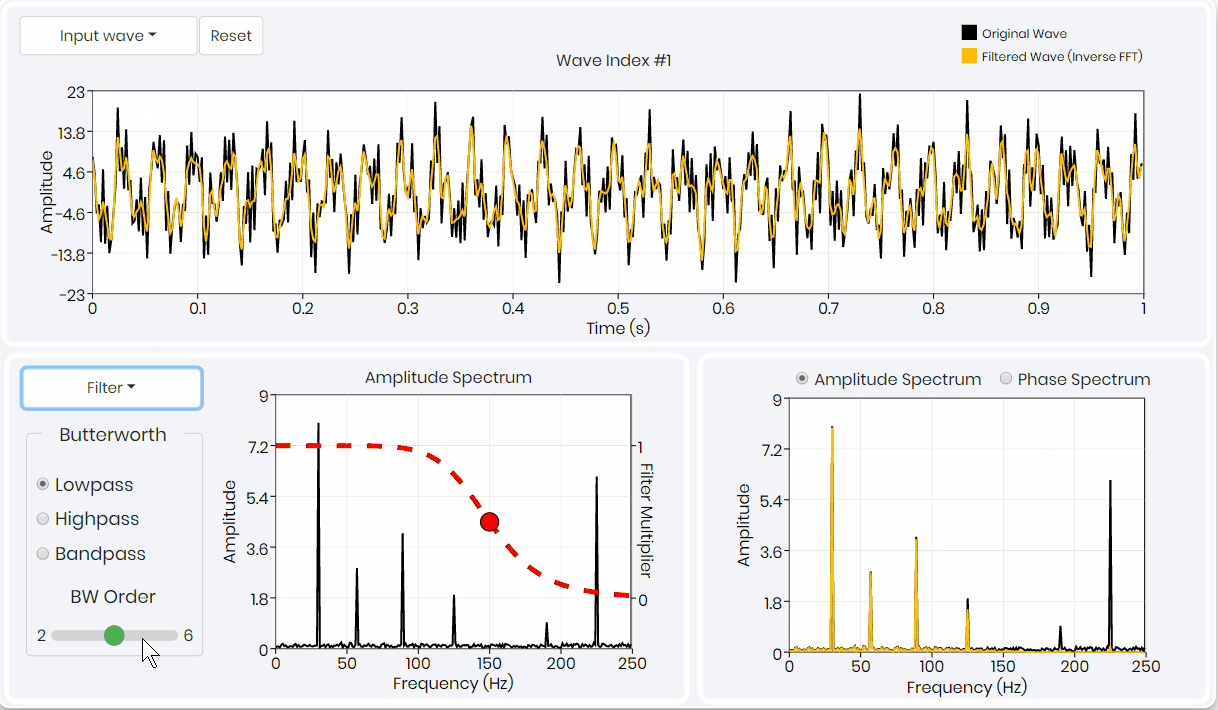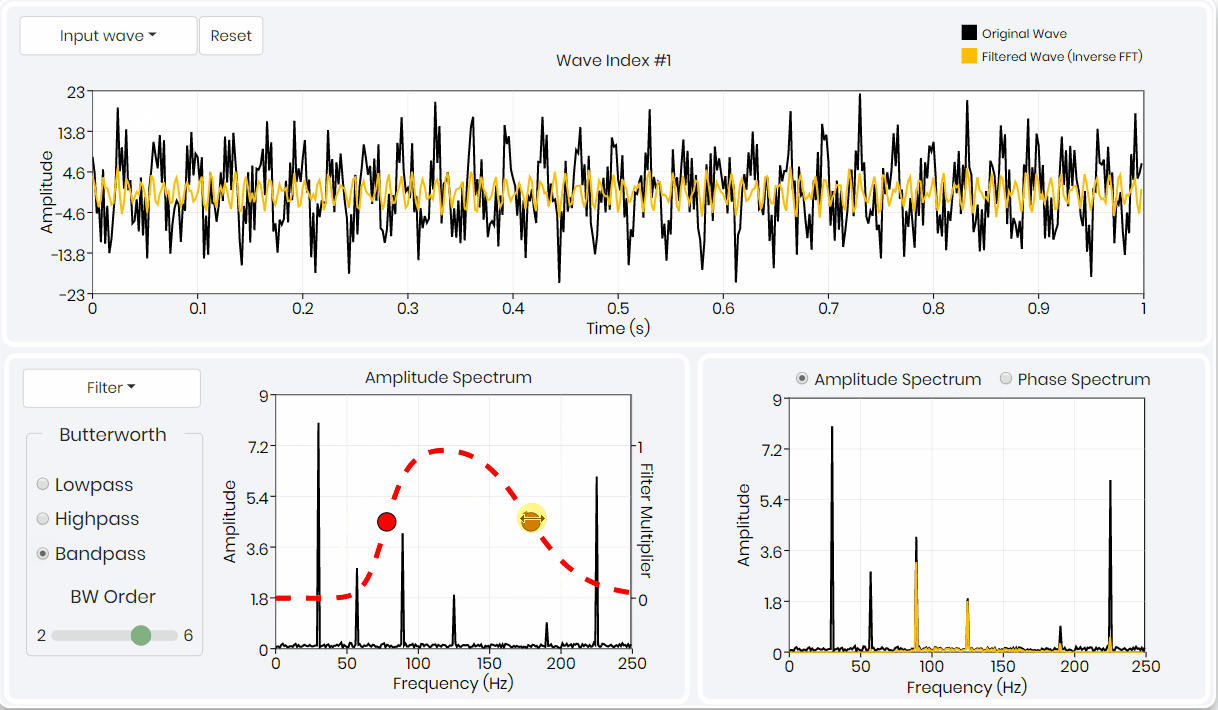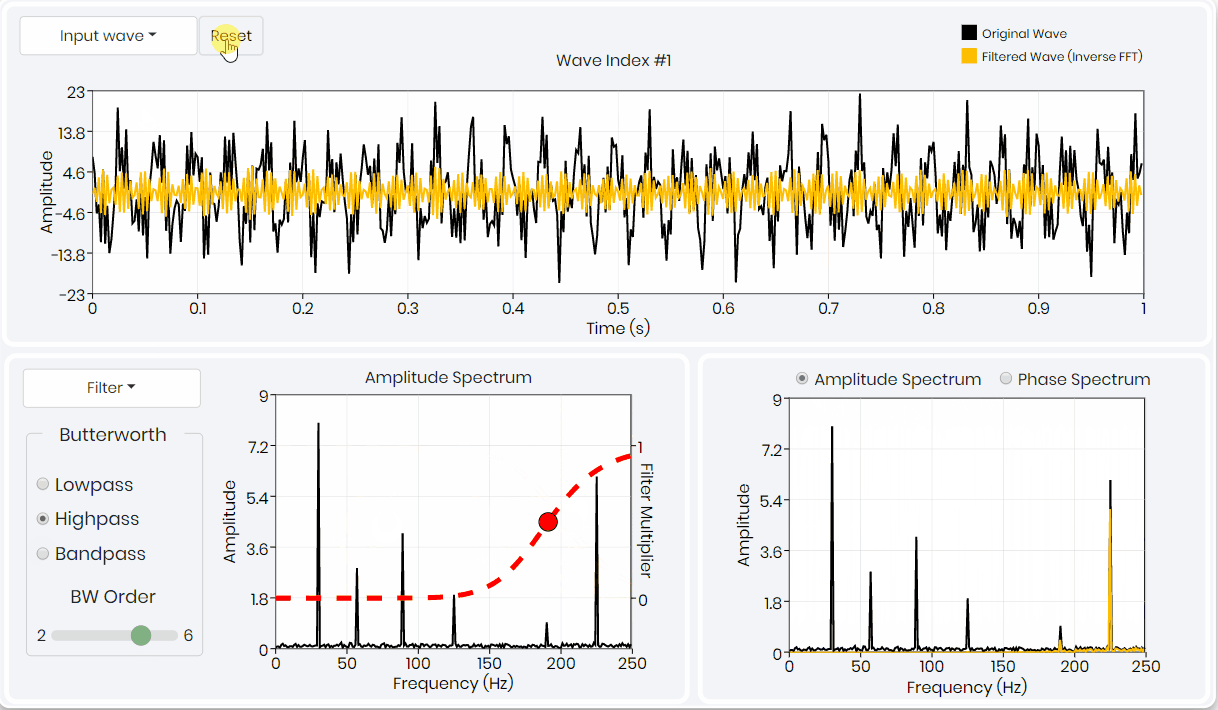
The goal here is to gain intuition into how a geophysical signal is characterized in the frequency-spectral domain and how to design and apply filters there. You will go through the various original signals and see the result of filtering using different filter types. You observe the part of the signal spectra that is changed with the filters and can compare the filtered signal with the original one in real-time..
Michael Burianyk, Scientific advisor
With “FFT Filtering” simulation you will get a chance to achieve:
- Understanding Fast Fourier Transform (FFT) analysis.
- Develop an appreciation of how filtering in the frequency domain is done.
- Understanding of three types of signal processing filters – Trapezoidal, Gaussian and Butterworth.
Want to have access to this simulation and explore by yourself? Contact us!
